| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 철도공학
- 운전이론
- 나무꾼이다솜
- 시드니기숙사
- 교환학생
- BOJ
- subclass500
- 백준
- 교통법규
- 호주휴대폰개통
- 열차운전
- UTS
- 교환학생짐싸기리스트
- 호주
- C++
- 철도교통안전관리자
- C
- 교환학생짐싸기
- c언어
- 교통안전관리론
- 호주학생비자
- scapesydneycentral
- 교환학생짐
- 호주비자신체검사
- 호주기숙사
- 1421번
- 군전세객차
- 시드니
- Scape
- 교통안전법
- Today
- Total
탐정사무소
2156번 포도주 시식(파이썬, 다이나믹 프로그래밍) 본문
최근 파이썬으로 자료구조 및 알고리즘 코테 연습을 하고 있는데, 다이나믹 프로그래밍 관련 문제들이 주로 나와서 풀고 있다. 오늘 푼 한 문제를 정리해보자.
https://www.acmicpc.net/problem/2156
문제
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다.
- 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
- 연속으로 놓여 있는 3잔을 모두 마실 수는 없다.
효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오.
예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.
사전지식
다이나믹 프로그래밍(Dynamic Programming, 동적계획법)은 분할정복처럼 큰 문제를 작은 문제로 쪼개는 알고리즘이지만, 작은 문제를 합쳐 큰 문제를 해결하는 상향식(bottom-up) 접근 기법이다. Memoization, 즉 기존에 푼 답을 테이블에 기억하고 이것을 큰 문제 풀이 시 재사용한다는 것이 특징이다. 최적화 문제(optimization problem) 풀이에 주로 사용가능하다. 지금까지 동적 프로그래밍으로 푼 문제의 예시 몇 개는 다음과 같다.
- 오르막 수: 수의 자리가 오름차순을 이루는 수. 오름 수의 최대 개수 구하기 (백준 11057)
- RGB거리: n개의 집이 나열되어 있을 때, 각 집들은 색이 달라야하며, 이 때 최소 비용 구하기 (백준 1149)
- 합분해: 0부터 n까지의 정수 k개를 더해서, 그 합이 n이 되는 경우의 수 구하기(최대 개수 구하기) (백준 2225)
- Matrix chain multiplication: 행렬 곱을 최소로 하는 경우 순서 찾기 (알고리즘 교재, 수업)
- Assmbly line scheduling: 두 공정 라인에서 최소 시간으로 생산하는 경우의 수 찾기 (알고리즘 교재, 수업)

또 알고리즘 수업에서 배운 것에 따르면, 이런 최적화 문제에는 2가지 특징이 있다. 증명은 전공 수업에서 했는데 생략한다.
(1) Optimal substructure property: Assume that an optimal solution. that consists of optimal solutions of the subproblems. 최적의 해답에는 최적의 부분문제들을 포함하고 있다.
(2) Overlapping subproblems property: same subproblem can be repeatedly solve again recursively. 즉 풀이 시 재귀적으로 이미 푼 같은 문제의 답을 이용하게 된다.
이러한 조건 만족 시 DP 알고리즘으로 문제 풀이 가능하다.
해결과정
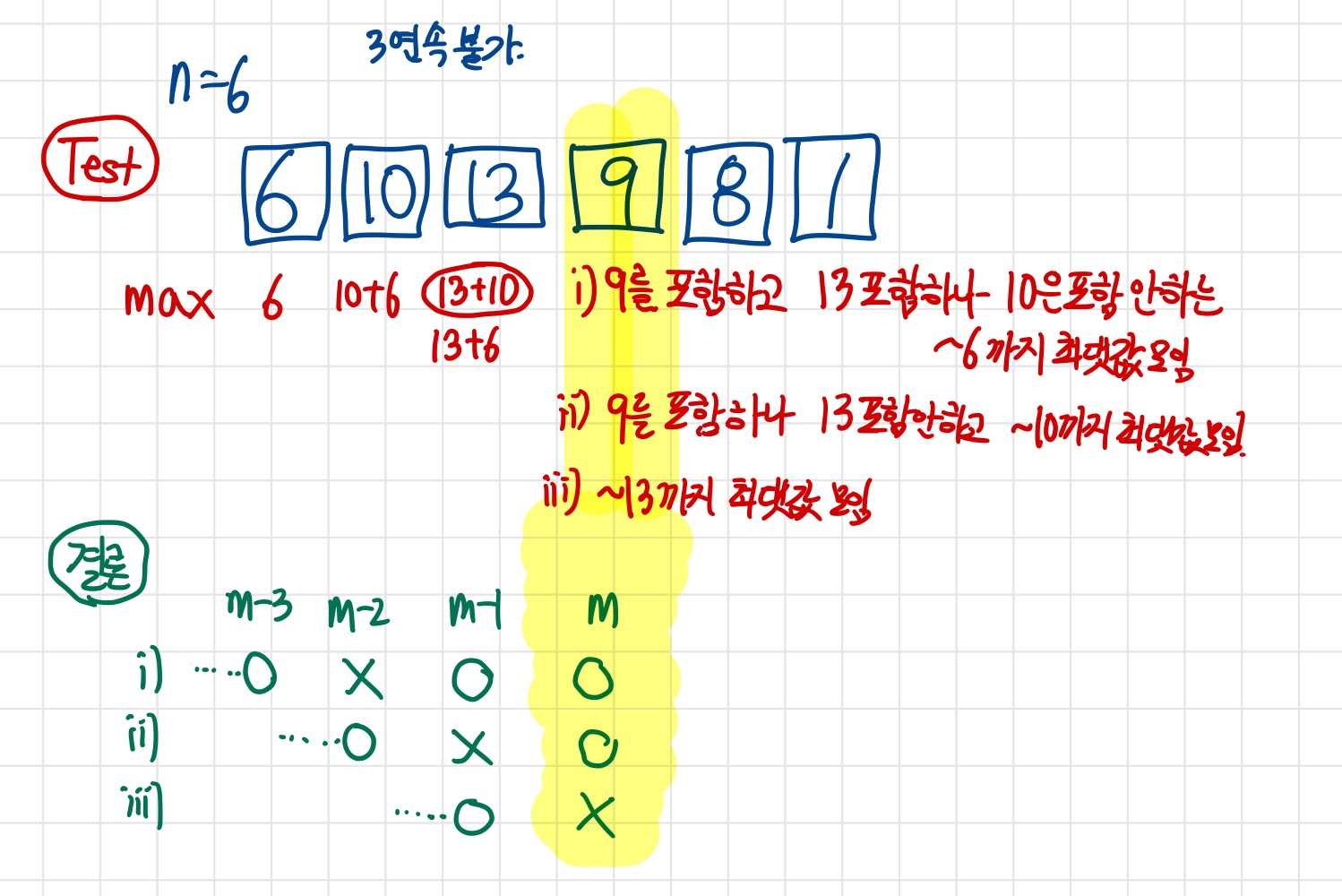
특정 위치까지의 최댓값을 구한 것은 그 다음 위치, 그 다다음 위치, 그다다다음 위치에까지 사용되는 overlapping 특성이 보이며, 각 단계마다 그 위치가 최적의 해라고 말할 수 있기 때문에 DP로 해결가능하다.
포도주가 1개, 2개, 3개 있을 때는 직접 계산해준다.
4개있을 때 부터가 핵심이다. 왜냐하면 3연속 포도주 선택이 불가하기 때문에 3이라는 숫자가 중요하기 때문이다. 이 상황에서도, 4개부터는 전부 패턴이 3가지로 동일하다.
1) 본인 포함, 본인-1 포함, 본인-2 미포함, 본인-3에서 구한 최댓값
2) 본인 포함, 본인-1 미포함, 본인-2에서 구한 최댓값
3) 본인 미포함, 본인-1에서 구한 최댓값
코드
import sys
n = int(sys.stdin.readline())
data = [0]
for i in range(n):
data.append(int(sys.stdin.readline()))
dp = [0] * (n+1)
dp[1] = data[1]
if n > 1:
dp[2] = data[1] +data[2]
if n > 2:
dp[3] = max(data[3] + data[2], data[3] + data[1], dp[2])
for i in range(4, n+1):
dp[i] = max(data[i] + data[i-1] + dp[i-3], data[i] + dp[i-2], dp[i-1])
sys.stdout.write(str(dp[n]))결과

DP는 코테, 알고리즘 고전 출제 알고리즘이니 양치기로 기술을 잘 익히자...
